선형대수 - 행렬의 종류에 대하여
- 복습,텐서의개념,대각행렬,단위행렬,정사각행렬,전치행렬
전에 올린 벡터기초 개념을 다시 복습하면서
행렬의 종류와 곱셈을 해보겠습니다
행렬(matrix)
스칼라(scalar)
벡터(vector)
영어 표기법은 알아두는것이 좋습니다
행렬이란
말 그대로 행(row) , 열(column)로 구성되어있습니다
가로를 행, 세로를 열 이라고합니다
행렬은 스칼라,벡터로 구성되어있습니다
스칼라란
행렬을 구성하는 요소인 각각의 숫자를 의미하고, 행렬의 구성중에서 가장 최소단위에 해당합니다
[ 0 1] a 행렬이 있다고 칩시다
a = |2 4| 0,1,2,4,3,0 은 스칼라입니다
[3 0]
벡터란
스칼라의 집합입니다
스칼라는 0,1,2,4 와 같은 크기만을 가지고있습니다.
반면 벡터는 방향과 크기둘다 모두 가지고있습니다
그리고 벡터는 크게 행벡터,열벡터로 나뉩니다
a = ( 1 5 ) a처럼 원소를 행 방향으로 나열한것을 행벡터
(1)
b = (3) b처럼 열방향으로 나열하면
(5) 열벡터
벡터는 거의 주로 열벡터로 표기합니다
다시 정리하자면
벡터는 스칼라의 집합입니다
벡터공간안에 스칼라가 있기때문입니다
그리고
행렬은 벡터의 집합입니다
(행렬은 행벡터의 집합이라고도 볼수있고,
열벡터의 집합이라고 볼수있습니다)
A = (1 5)
(3 4) 행렬 A를 행벡터로 나타내면
(5 2) (1 5) , (3 4), (5 2)
행렬A 열벡터로 나타내면
2차원 평면에 3개의 벡터가 존재 한다고 생각할수도있습니다
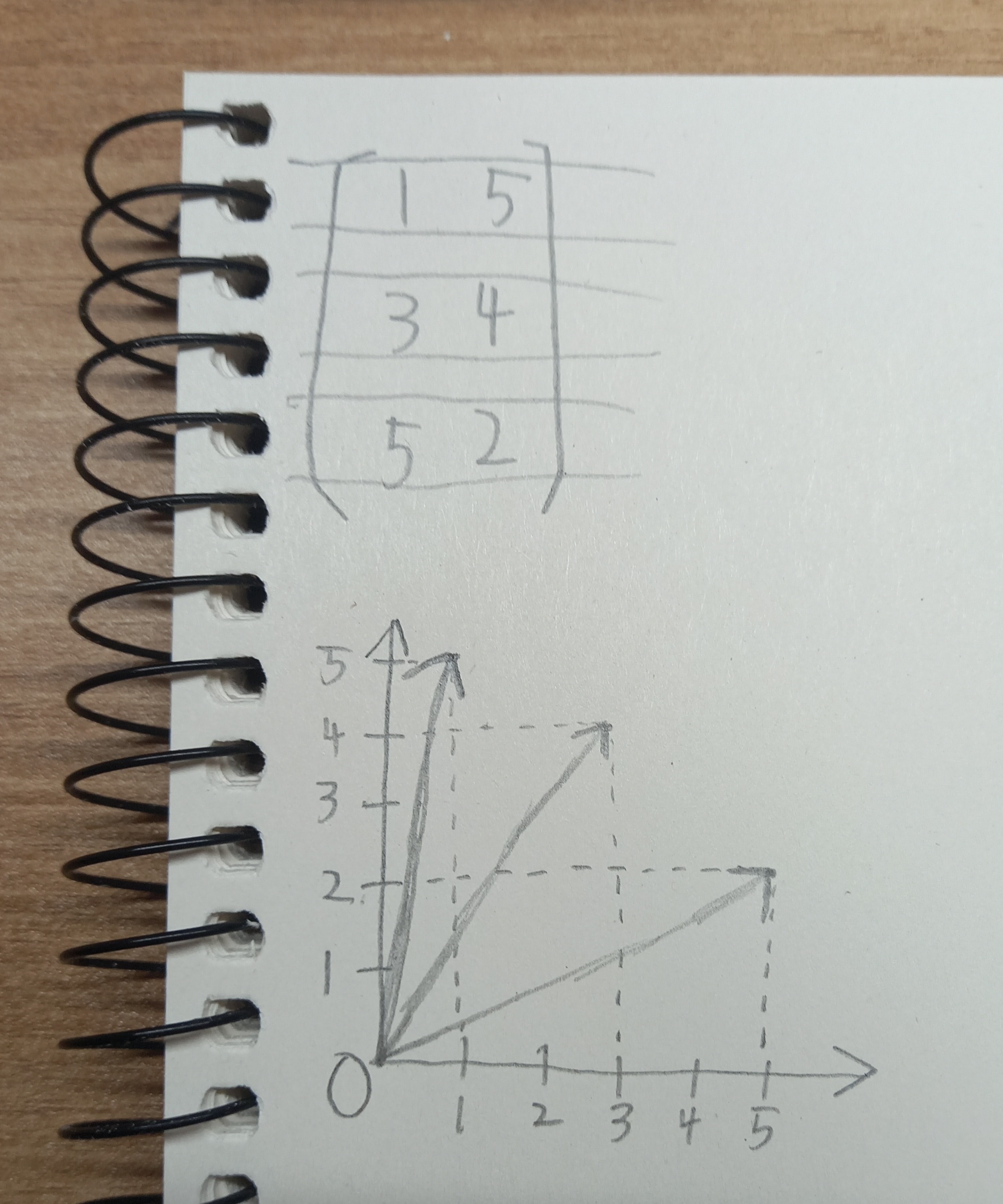
행렬A가
(1) (5) 이렇게 열벡터의 결합의 형태
(3) ,(4) 입니다
(5) (2)
이거를 3차원공간의 2개의 벡터라고 생각할수있습니다
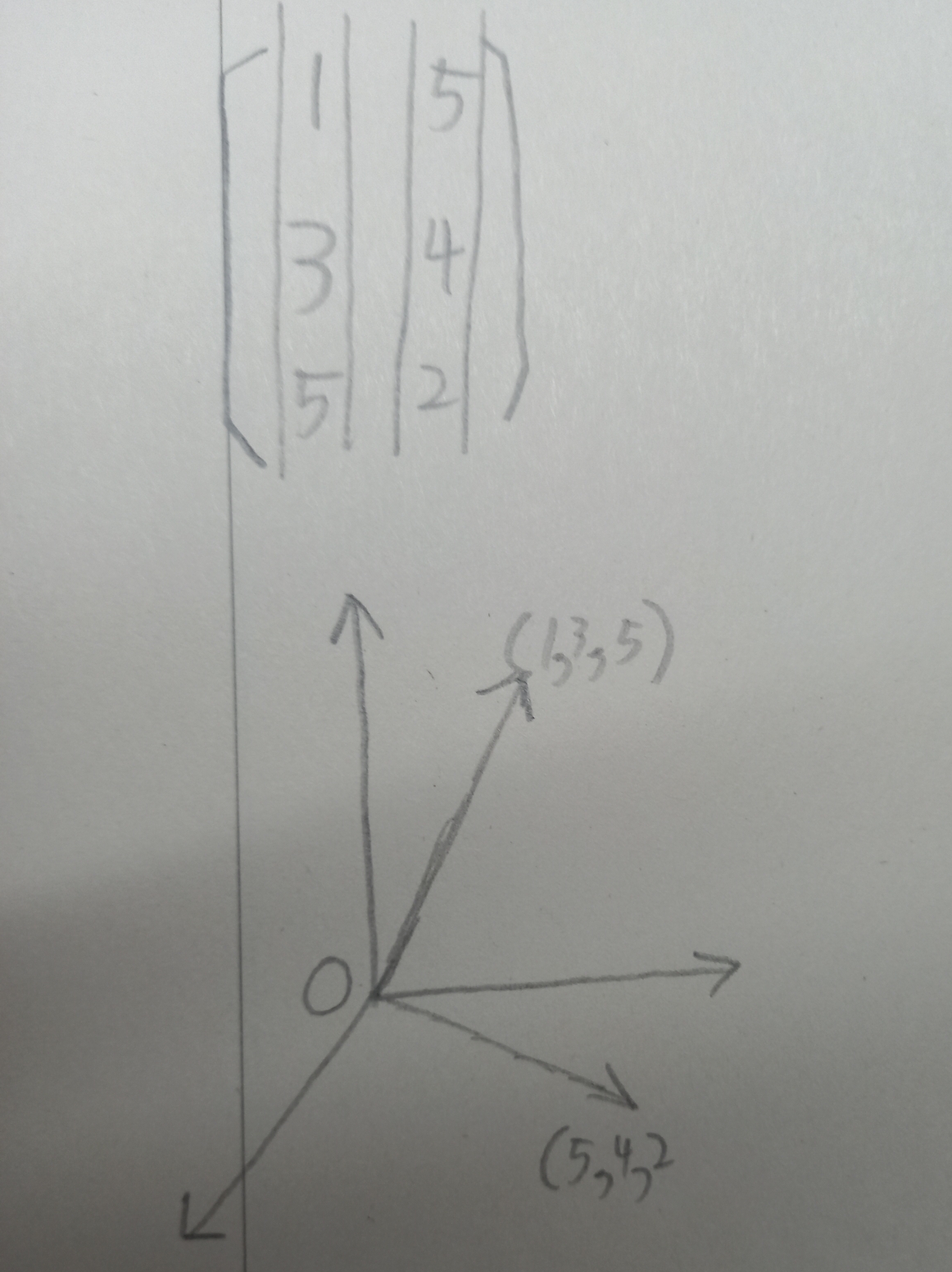
이렇게 같은 행렬이더라도 어떠한 관점으로 보는지에 따라 다르게 표현할수있습니다
행렬을 구성하는 각 스칼라값을 행렬 원소(matrix element) 라고합니다
행렬을 구성하는 원소는 행번호와 열번호를 사용하여 표기합니다
ex) 원소a를 스칼라형태로 쓰고 오른쪽아래 작게 행번호,열번호순으로 표기합니다
aij -> a는 스칼라 , 행번호는 i , 열번호는j
행렬의 크기는 행렬의 행수와 열수로 나타냅니다
(a11 a12)
(a21 a22) 3개의 행(row(가로))와2개의열(colu
(a31 a32) mn(세로))
이렇게 행렬을 직접보면 이해하기 쉬울겁니다
그러므로 이 행렬은
행 × 열 , 즉 3 × 2 가 이 행렬의 크기라고 표기할수있습니다.
여태 행과열로 구성되있는 기본적인 2차원 행렬에 대해 알아보았습니다
그렇다면 n차원 행렬은 어떨까요?
행과 열 2차원으로 구성된 행렬이 아닌 n차원으로 일반화한 행렬을 텐서(Tensor) 라고 부릅니다
텐서 어디서 익숙하다는 느낌이 드나여?
파이썬에는 텐서플로우 라는 라이브러리가 존재합니다
텐서는 머신러닝,딥러닝라이브러리인 텐서플로우라는 이름에서 유래된 이름입니다
텐서플로우는 텐서의 흐름을 다루는 라이브러리입니다
스칼라 -> 1
(scalar)
벡터 -> (1)
(vector) (3)
행렬 -> (1 2)
(matrix) (3 4)
텐서 -> ( (1 2) (5 6) )
(Tensor) ( (3 4) (7 8) )
( (2 3) (4 1) )
( (5 7) (2 3) )
대각행렬이란
대각 행렬(diagonal matrix) 는 행렬의 대각 원소이외의 모든 성분이 0인 행렬을 의미합니다
이해를 돕기위해 행렬을 그려보겠습니다
( 2 0 0 )
D = ( 0 3 0 )
( 0 0 7 )
단위행렬이란
단위행렬(identity matrix) 는 행번호와 열번호가 동일한 대각선의 원소가 모두 1이며 나머지 원소는 모두 0으로 표기하여 정사각 행렬(square matrix)
를 의미합니다 정사각행렬은 행과 열의 크기와 같은 행렬의 의미합니다
이것도 이해를 돕기위해서 행렬을 그려보겠습니다
( 1 0 0 )
I = ( 0 1 0 )
( 0 0 1 )
D행렬은 대각행렬 diagonal matrix 에 앞에 철자 D를 따서 주로 명칭으로 씁니다
I행렬은 단위행렬 identity matrix 에 앞에 철자
I를 따서 주로 명칭으로 씁니다
대각행렬과 단위행렬은 선형대수에서 중요한 개념이므로 머리에 콕 박아두시길 바랍니다
왜냐하면 행렬을 이용해서 계산을 할때는 연산량이 많아질수있는데 행렬을 대각행렬이나 단위행렬로
변환한다면 연산량이 줄어들어서 모델을학습시간을 줄이고 시스템의 자원을 아낄수도있습니다
이제 이글의 마지막부분인 전치 행렬입니다
(1,2분만 더 화이팅!)
전치 행렬이란
전치행렬 (Transposed matrix)은 기존행렬의 행과 열을 바꾸는거를 뜻합니다.
앞에서 보았던 aij 의 행과 열을 바꿔서
aji로 표현하는게 전치행렬입니다
ex) 3 × 2 행렬을 전치시켜서 2 × 3 행렬이 됩니다
그리고 행렬의 각 원소의 행번호와 열번호가 서로 바뀝니다 그리고 전치행렬을 Transposed의 스펠링 앞 철자를 따서 대문자 T 로 표기합니다
이해를 돕기위해서 그려보겠습니다
( 1 5 )
A = ( 3 4 )
( 5 2 )
( 1 3 5 )
A^T = ( 5 4 2 )
이렇게 2 ×3 의행렬을 3 × 2로 전치시켜서 행벡터가 됩니다
이것을 더 깊숙하게 이해할려고한다면
( a11 a12 )
( a21 a22 )
( a31 a32 )
( a11 a21 a31 )
( a12 a22 a32 )
로 나타낼수있습니다
결론은
원래 행렬과 전치 행렬의 행렬 원소의 행 번호와 열 번호를 보면 서로 바뀌어 있는 것을 볼수있습니다
/ 끝까지 읽어주어 감사합니다
/ 내일 글을 이어서 올라올지는 모르겠지만
/ 자고 내일 한번 생각해보져(?)
/ (머신러닝),(딥러닝) 열심히 공부해서 모두 마스터하는 날 까지!
끝내자! 머신러닝 딥러닝